이 멋진 흑마법에 축복을! 2

Q_rsqt

알림!

이 글은 국방망 내 대한민국 해군 1함대 지휘통신대대 자유게시판에 게시한 내용을 베껴 적은 뒤 오타 및 비문만 수정한 글입니다. 실제 작성일은 2022년 4월 1일입니다.

필승! 불철주야 당직근무에 고생하시는 전국의 수병님들, 오늘도 안전항해를 기원합니다.

요즘 MP3에 넣어놓은 노래가 하나둘씩 증발하는 바람에 소형 스포티파이 플레이어를 직구로 구매할까 진지하게 고민중인 674기 참치입니다. 개당 80달러나 하는데, 솔직히 저 돈 주고 살 거면 아이리버제 DAP를 살 텐데 말입니다… 그리고 아이리버 DAP를 살 거면 소니 워크맨을 사는 게 더 낫지 않나…

개인적으로는 소니가 오디오 기기를 참 잘 만든다고 생각합니다. 노이즈캔슬링 성능도 좋고, 베이스부터 트레블까지 깔끔하게 뽑아주니… 이번에 링크버즈를 주문해서 다음에는 한번 링크버즈 리뷰라도 해 볼까 합니다.

~~스포티파이 Hi-Fi 나올때까지 숨참기! 흡!!!!!~~

수병님들은 "흑마법"이라는 단어를 들으면 어떤 이미지가 떠오르십니까? 오른손의 흑염룡이 깨어난다든가…?

"흑마법"이라는 단어가 씹ㄷ… 프로그래밍 업계 은어로 들리지만 의외로 외국에서도 통용되는 말입니다. 구글에 "black magic"나 "wizardry"라고 검색해도 꽤 결과가 나오고… 해커 뉴스 같은 곳이나 레딧에서도 심심찮게 보이죠.

역시 사람 사는 곳은 거기서 거기인가 봅니다.

아무튼, 저번에 예고했던 대로, 오늘의 흑마법은 프로그래밍 업계의 살아있는 전설, 존 카맥이 만들었다고 전해지는 알고리즘, Fast Inverse Square Root입니다.

John Carmack, Id Software, 그리고 Quake III Arena

이 알고리즘은 너무나도 유명한 탓에 알고 계신 분들도 많을 거라 생각합니다. 하지만 내부 구조와 그 원리까지 들여다보면 참 심오한 알고리즘입니다.

수병님들은 Id Software라는 회사를 알고 계십니까?

만약 콘솔 게임을 좋아하시거나, 고전 게임을 좋아하시거나, 하드웨어 해킹 쪽에 발을 담가 봤다거나, ~~나이가 많다거나~~ 하다면 아실지도 모르겠습니다.

Id Software는 게임 개발 스튜디오로, 이 회사의 대표작으로는 DOOM과 Wolfenstein 시리즈가 있습니다.

네, 냉장고부터 ATM기, 프린터에 심지어 맥북 프로 터치 바에서까지 안 돌아가는 곳이 없는 바로 그 DOOM의 제작사 맞습니다.

이 회사에서 만든 게임 중 "3D 슈터"라는 새로운 장르를 개척하는 데 일조한 게임이 있는데, 바로 Quake 시리즈입니다. DOOM 시리즈의 계보를 잇는 Quake부터, 완전 3D 환경에서의 FPS를 구현한 Quake II, 그리고 그동안의 스토리 위주 게임플레이에서 멀티플레이어 전용이라는 대담한 선택을 한 Quake III Arena까지, 모두 고전 FPS의 명작입니다.

특히, Quake III Arena에서 사용된 엔진은 그냥 3D 물체에 텍스처만 입히던 지난 엔진과 달리, 실시간 셰이딩을 지원하는 새로운 기술을 선보여 더욱 화제에 올랐었습니다.

게임 출시 후 몇 년이 지나고, 2002년경 유즈넷 등지의 몇몇 포럼에서 Quake III Arena의 실시간 셰이딩 기법에 관한 이야기가 화제가 된 적이 있습니다.

그 중에서 존 카맥이라는 프로그래머가 작성한 어떤 함수 하나가 사람들의 이목을 잡아끌었는데요, Q_rsqt라는 이름을 가진 이 함수는 수학 관련 코드에서 발견되었고, 곧 이 알고리즘은 Fast Inverse Square Root라고 불리게 됩니다.

Fast Inverse Square Root, 직역하면 겁나 빠른 제곱근의 역인데, 말이야 어렵지만 식은 아래와 같이 간단합니다.

\begin{equation*} f(x) = \frac{1}{\sqrt{x}} \end{equation*}

말 그대로 어떤 수의 제곱근의 역수를 겁나 빠르게 구하는 알고리즘에 불과하니까 말이에요.

언뜻 보면 되게 이상한 곳에서 최적화를 하려고 하는 것 같습니다. 기본적으로 최적화는 1) 자주 쓰이는 연산이 2) 느릴 때나 하는 거잖습니까?

묘-하게 써먹기 힘들어 보이는 이 단항식이 얼마나 자주 사용되길래, 또 얼마나 느리길래 흑마법까지 부릴 필요가 있는 걸까요?

게임 엔진을 건드려 보신 분들이라면 금방 아시겠지만, 컴퓨터에서 3D 환경을 구현할 때는 벡터의 존재가 필요불가결합니다. 물체의 위치나 움직임은 물론이고, 색상 등을 계산해서 장면을 렌더링할 때도 벡터가 사용되기 때문입니다.

여기서 벡터는 크기와 방향, 두 가지의 구성요소로 이루어진 값인데, 하나의 벡터에서 방향 정보만 뽑아내야 하는 경우가 가끔 있습니다. 어떤 게임오브젝트의 속력에서 방향만을 추출해서 다른 연산에 사용하는 경우도 있겠지만, 가장 자주 사용되는 경우는 셰이딩일 겁니다.

셰이딩, 즉 그림자를 그릴 때는 빛이 어떤 3D 물체 표면에 닿는 입사각으로부터 반사각을 구해야 합니다. 이때 필요한 것이 표면 법선벡터(surface normal)입니다.

표면 법선벡터는 3D 트라이앵글 하나에 수직인 벡터를 말하는데, 이 벡터는 방향 정보만을 가지고 있습니다. (이 부분에 대해서는 나중에 레이트레이싱 시리즈에서도 이야기해 보겠습니다.)

어떤 벡터의 "방향"만이 필요하다면 벡터곱 연산에서 크기의 영향이 없도록 크기를 1로 만들어 주는 게 좋습니다. 이 과정을 정규화(normalization)라고 하는데, 어떤 벡터 $\vec{v}$ 에 대한 정규화 식은 아래와 같습니다.

\begin{equation*} \text{normalize}(\vec{v}) = \frac{\vec{v}}{||\vec{v}||} \end{equation*}

여기서 분모에 보이는 벡터의 "절댓값"으로 보이는 값이 있는데, 이 값은 벡터의 놈(norm)이라고 불리는 값입니다. 3차원 벡터 $\vec{v} = \langle x, y, z \rangle$ 에 대하여 놈 $||\vec{v}||$ 는 아래와 같이 정의됩니다.

\begin{equation*} ||\vec{v}|| = \sqrt{x^2 + y^2 + z^2} \end{equation*}

위 정의를 정규화 식에 집어넣어 보면 어떤 수의 제곱근의 역수에 벡터가 곱해진 꼴이 된다는 것을 볼 수 있습니다.

화면에는 엄청나게 많은 픽셀이 있고, 또 어떤 3D 씬 안에는 많은 폴리곤으로 이루어진 3D 메시가 배치되어 있다는 점을 생각해보면, 게임 엔진은 게임을 실행하는 내내 1초에 수백, 수천 번이나 어떤 수의 제곱근의 역수를 구해서 벡터에 곱하는 연산을 수행하고 있다는 사실을 알 수 있습니다.

이렇게 자주 사용되는 연산이니 당연히 프로그래머는 이 연산을 최대한 간결하게 코드로 바꿔야 할 겁니다. 만약 수병님들이라면 어떻게 작성하시겠습니까? 저라면 간단하게 C로 아래와 같이 짤 것 같습니다.

#include <math.h>

inline float inverse_sqrt(float number)
{
    return 1.0f / sqrt(number);
}

일반적인 상황에서는 위 코드도 나쁜 코드는 아닙니다. 간결하고 직관적이니 별다른 주석도 필요 없을테고, 표준 라이브러리가 제공하는 기능이니 안정성과 정확도 면에서는 믿고 맡길 수 있죠.

그러나 여기서 짚고 넘어가야 할 점이 있습니다. 부동 소수점 연산은 느리다는 것입니다.

논리적 가산기로 사칙연산을 구현할 수 있는 정수와는 달리, 부동 소수점 연산은 지수부와 가수부를 모두 고려해야 하므로 연산이 훨씬 복잡합니다. 우리가 사용하는 컴퓨터에 들어가는 범용 CPU 안에는 이 연산에 특화된 FPU가 바로 이 때문에 구비되어 있습니다.

컴퓨터로 제곱근을 계산하는 방법 중 가장 일반적인 방법은 뉴턴-랍슨 근사법(Newton-Raphson method)을 이용하는 방법입니다. 이 방법은 어떤 함수의 근을 근사하는 방법으로, 미분 가능한 함수 $f$ 에 대하여 어림값 $x_n$ 으로부터 더 정확한 어림값 $x_{n + 1}$ 을 아래와 같이 구해냅니다.

\begin{equation*} x_{n + 1} = x_n - \frac{f(x_n)}{f'(x_n)} \end{equation*}

위 식을 컴퓨터로 계산할 경우, 계산에 사용되는 식이 모두 부동 소수점 실수고, 똑같은 연산을 수차례 반복해야 정확한 결과를 얻을 수 있으므로 연산 시간이 길어지게 됩니다. 실시간으로 이런 연산을 수없이 실행해야 하는 게임 엔진에게는 적합하지 않은 방법이죠.

대체 카맥은 어떤 방식으로 이 연산을 최적화했길래 그렇게나 사람들의 이목을 끈 걸까요?

알고리즘 훑어보기

아래는 실제 Quake III Arena 소스코드에서 필요 없는 매크로 등만 삭제한 코드입니다.

float Q_rsqt(float number)
{
    long i;
    float x2, y;
    const float threehalfs = 1.5f;
    x2 = number * 0.5f;
    y = number;
    i = *(long *)&y;                        // evil floating point bit level hacking
    i = 0x5f3759df - (i >> 1);              // what the fuck?
    y = *(float *)&i;
    y = y * (threehalfs - (x2 * y * y));    // 1st iteration
//  y = y * (threehalfs - (x2 * y * y));    // 2nd iteration, this can be removed
    return y;
}

……어디서부터 건드려야 할지 막막합니다.

점심을 나가서 먹어야 할 것 같은 포인터 캐스팅부터, 의미를 알 수 없는 16진수 숫자에, 주석에는 욕까지 쓰여 있고… 눈이 아주 즐겁습니다.

자, 한 번에 풀기에 너무 큰 문제에 직면하면 어떻게 해야 할까요?

그렇습니다. 잘게 쪼개가지고 야금야금 공략하면 됩니다!

그럼 이 알고리즘을 세 조각으로 divide and conquer 해보겠습니다.

step 1. evil floating point bit level hacking

C에서 float 타입은 IEEE 754 표준을 따르는 binary32 실수입니다…라고 하면 말이 너무 어려우니까 단계적으로 가 보겠습니다.

컴퓨터에서 실수를 표기하는 방법은 고정 소수점 실수, 부동 소수점 실수 두 가지가 있습니다.

여기서 부동은 한자로 不動이 아니라 浮動이라고 쓰는데, 말 그대로 소수점이 둥둥 떠서 움직이는 실수가 되겠습니다.

그런 의미에서 헷갈리지 않도록 지금부터 둥둥 소수점 실수라고 부르겠습니다. (실제로 저는 이렇게 부릅니다…)

여기서 소수점이 둥둥 떠다닌다는 게 무슨 뜻인지 감이 잘 안 오실 겁니다.

사실 그렇게 어려운 개념은 아닌 게, 과학적 기수법(scientific notation)을 생각하시면 편합니다.

과학적 기수법은 매우 큰 수나 매우 작은 수를 효율적으로 나타낼 수 있는 표기법인데, 공학용 계산기에서 자주 볼 수 있습니다.

예를 들어, 0.000000000000000137284라는 수를 표현할 때 1.37284e-16이라고 쓰고, 137284000000000000000000000이라는 수를 표현할 때 1.37284e21이라고 쓰는 게 바로 과학적 기수법입니다. 훨씬 간결하죠!

위 예시를 보면 1.37284라는 "가수부"는 같은데 뒤에 지수만 다르게 해서 수를 표현하고 있다는 사실을 알 수 있습니다. 즉, e 다음에 나오는 숫자만큼 소수점을 앞뒤로 움직인다고 볼 수 있겠습니다. 소수점이 둥둥 떠 있는 것처럼요!

IEEE 754 표준에서 정의하는 둥둥 소수점 규격은 이 과학적 기수법의 이진수 버전이라고 생각하시면 편합니다. 특히, binary32는 32비트로 둥둥 소수점 실수를 표현하는 방식으로, 32비트를 3개의 구역으로 나눕니다.

최상위 비트 하나는 부호 비트 (0이면 양수, 1이면 음수)
그 다음 상위 8개 비트는 지수부 (8비트 부호 없는 정수에 편항치 -127)
나머지 23비트는 가수부

여기서 가수부는 과학적 기수법에서 e 앞에 오는 부분입니다. 그러니 가수부에 할당된 비트가 많을수록 더 정밀한 수를 표현할 수 있겠죠?

과학적 기수법의 규칙에 따라, 가수부의 정수부는 항상 한 자리여야 하므로 가수부는 22비트만큼의 정확도를 가진다고 할 수 있겠습니다.

사실 가수부의 정확도는 23비트라는 점만 빼면 말이죠……

규칙상 가수부의 정수부는 0이 아닌 수여야 합니다. 하지만 이진수에서 0이 아닌 수라고 하면 1밖에 없지 않습니까? 이를 이용하면 가수부의 정수부를 항상 1이라고 하기로 약속하고, 23비트를 모두 소수부에 쏟아부을 수 있게 됩니다!

예를 들어, 00111110001000000000000000000000₍₂₎이라는 32비트 값을 binary32 수로 해석해 보겠습니다.

최상위 비트가 0이니 양수고,
01111000₍₂₎ = 124₍₁₀₎인데, 여기서 편향치 -127을 적용하면 124 - 127 = -3이니 곱할 수는 2^-3이고,
가수부에 정수부 1을 붙이면 1.01000000000000000000000₍₂₎ = 1.01₍₂₎ = 1.25₍₁₀₎

따라서 이 이진수 실수는 1.25 * 2^-3 = 0.15625를 표현한 것입니다!

이정도면 다른 부분을 이해하기 충분할 테니 binary32에 대한 설명은 이쯤 하고 다시 원래 코드로 돌아가 보겠습니다.

여기서 우리는 악랄하게 둥둥 소수점 실수를 둥둥 소수점 실수로 생각하지 않고, 정수로 생각해서 연산할 겁니다.

즉, 둥둥 소수점 실수의 비트 표현식을 정수로서 해석하고자 한다는 것인데요, C언어의 일반적인 캐스팅으로는 이런 짓을 할 수가 없습니다.

예를 들어, float 타입 변수 f에 대하여 long f_as_long = (long)f; 문을 실행하면 컴파일러가 알아서 소수부를 떼어내서 정수로 바꿔주기 때문입니다.

바로 여기서 포인터 흑마법이 등장합니다.

i = *(long *)&y; // evil floating point bit level hacking

&y의 타입은 float 포인터입니다. 하지만, 내부적으로 포인터는 size_t만큼의 크기를 갖는 부호 없는 정수기 때문에, 포인터의 타입은 컴파일러가 타입 체크를 수행하기 편하게 하기 위한 도우미에 불과합니다. 어떤 포인터를 따라가면(dereference) 무슨 타입의 값이 나오는지 알려줄 뿐이죠.

그래서 &y를 long 포인터로 해석하게 되면 컴파일러는 &y가 가리키는 주소에 있는 32비트 값이 long 타입이라고 생각하게 됩니다. 사실 실제로 집어넣은 값은 32비트 둥둥 소수점 값인데도 불구하고 말입니다!

마지막으로 long 포인터로 해석한 &y를 따라가면 y에 담겨 있는 둥둥 소수점 데이터가 long 타입의 정수로 해석되어 i에 저장됩니다!

11번 줄을 보시면 다시 한번 이런 작업을 거쳐 연산이 끝난 i 값을 다시 float 타입으로 해석하는 것을 볼 수 있습니다.

y = *(float *)&i;

타입의 방향이 반대라는 점을 빼면 완전히 똑같은 모양이죠!

이렇게 내부적인 비트 표현식을 다른 타입으로 바꿔서 생각하는 것을 타입 말장난(type punning)이라고 부릅니다.

조금 더 이해하기 쉽게 쓴다면 union 타입을 사용할 수 있겠네요.

float Q_rsqt(float number)
{
    long i;
    float x2;
    union { long as_long; float as_float; } y;
    const float threehalfs = 1.5f;

    x2 = number * 0.5f;
    y.as_float = number;
    y.as_long = 0x5f3759df - (y.as_long >> 1);                               // what the fuck?
    y.as_float = y.as_float * (threehalfs - (x2 * y.as_float * y.as_float)); // 1st iteration
//  y.as_float = y.as_float * (threehalfs - (x2 * y.as_float * y.as_float)); // 2nd iteration

    return y.as_float;
}

(사실 이것도 UB입니다…)

step 2. what the fuck?

이 코드의 가장 이상한 부분이 드디어 등장했습니다. 얼마나 이상하면 코드 작성자도 주석으로 욕을 달아놨을까요?

문제의 코드는 10번 줄의 이 부분입니다.

i = 0x5f3759df - (i >> 1); // what the fuck?

시프트 연산자는 왜 나오고, 저 이상한 상수는 어디에서 튀어나온 걸까요?

저 흑마법을 이해하려면 이 함수 자체를 조금 analytic(?)하게 접근해야 합니다.

이번 단계에서는 매우 두렵게도 수식을 사용해야 합니다.

심호흡하고…

내쉬고…

들이쉬고…

내쉬고…

시작하겠습니다.

자, 우리가 구하고자 하는 제곱근의 역수를 $f(x)$ 라고 두겠습니다.

이 함수의 매개변수 $x$ 는 binary32 형식에 맞게 풀어내 보고, 같은 비트 문자열을 정수로 해석하면 나오는 수를 $x'$ 이라고 하겠습니다. $M$ 은 mantissa, 즉 가수부를 정수로 해석한 값이고, $E$ 는 exponent, 즉 지수부를 정수로 해석한 값입니다.

\begin{equation*} \begin{aligned} f(x) &= \frac{1}{\sqrt{x}} \\ x &= \left( 1 + \frac{M_x}{2^{23}} \right) \cdot 2^{E_x - 127} \\ x' &= E_x \times 2^{23} + M_x \end{aligned} \end{equation*}

일단 만만한게 로그니까 무지성으로 때려 박고 시작하겠습니다. 양변에 로그를 먹이고 우변의 지수를 풀어냅니다. 왜 하필 로그를 꽂아넣냐면… 어… 그냥…? 아무튼 꽂으면 뭔가 됩니다. 수능 풀 때도 무지성으로 꽂으면 뭔가 됐었던 기억이 나는데…

\begin{equation*} \begin{aligned} \log_2(f(x)) &= \log_2 \left( \frac{1}{\sqrt{x}} \right) \\ &= \log_2 \left( x^{-\frac{1}{2}} \right) \\ &= -\frac{1}{2} \log_2(x) \end{aligned} \end{equation*}

여기서 $x$ 를 binary32 형식으로 치환하고 다시 지수를 풀어냅니다.

\begin{equation*} \begin{aligned} \log_2(f(x)) &= -\frac{1}{2} \log_2(x) \\ &= -\frac{1}{2} \log_2 \left[ \left( 1 + \frac{M_x}{2^{23}} \right) \cdot 2^{E_x - 127} \right] \\ &= -\frac{1}{2} \left[ \log_2 \left( 1 + \frac{M_x}{2^{23}} \right) + \log_2 \left( 2^{E_x - 127} \right) \right] \\ &= -\frac{1}{2} \left[ \log_2 \left( 1 + \frac{M_x}{2^{23}} \right) + E_x - 127 \right] \end{aligned} \end{equation*}

흠… 뭔가 많이 풀어지기는 했지만 여기서 더 나아가기는 조금 힘들어 보입니다. 로그를 풀어낼 수 있을 만한 건덕지가 보이지 않네요.

여기서 발상을 전환해 보겠습니다.

지금부터 저희는 수학자의 마인드를 버리고 공학자의 마인드를 장착하겠습니다.

그리고 공학자의 마인드는 한 가지의 전제를 깔고 들어가는데 그건 바로…

무지성 근사입니다.

아니, 어차피 컴퓨터가 제곱근을 무한한 정밀도로 계산할 수 없는 시점에서 순수 수학이 아니지 않습니까? 그러면 그냥 대충 살아도 되지 않나……

그런 의미에서 저는 $[0, 1)$ 구간에서 $y = \log_2(1 + t)$ 를 일차함수 $y = t$ 로 무지성 근사해 버리겠습니다. 왜냐하면 이 구간에서는 두 함수의 모양이 비슷하기 때문입니다!!! ( $\sin(x)$ 마저도 $x$ 로 근사해 버리는 공학의 세계에서 이 정도는 아무것도 아닙니다…)

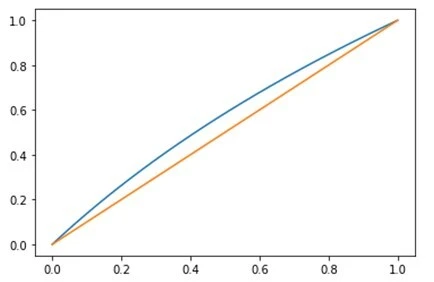
생각보다 두 그래프가 상당히 가깝게 있다는 점을 보실 수 있습니다. 하지만 가운데, 0.5 근처에서는 상당히 차이가 벌어지니 조금 보정할 필요는 있어 보입니다. 그러니 일차함수 $y = t$ 에 보정값 $\mu$ 를 더해서 계산해 주겠습니다. 적당한 값 $\mu$ 를 고르면 그래프가 아래처럼 바뀝니다!

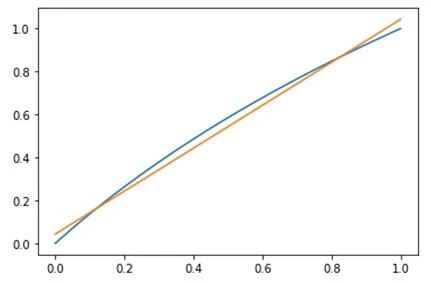
위 편법을 사용해서 식을 더 전개해 주겠습니다!

\begin{equation*} \begin{aligned} \log_2(f(x)) &= -\frac{1}{2} \log_2(x) \\ &\approx -\frac{1}{2} \left[ \frac{M_x}{2^{23}} + \mu + E_x - 127 \right] \\ &= -\frac{1}{2^{24}} \left( M_x + 2^{23} E_x \right) - \frac{1}{2}(\mu - 127) \\ &= -\frac{1}{2^{24}} \cdot x' - \frac{1}{2}(\mu - 127) \end{aligned} \end{equation*}

아니, 놀랍게도 둥둥 소수점 실수 $x$ 의 정수 표현식인 $x'$ 이 튀어나오는 것이 아니겠습니까?!?!?!?!?!?!

이제 거의 다 끝났습니다.

우변의 로그는 정리했는데, 좌변의 로그는 아직 살아있으니 이 친구의 목도 깔끔하게 잘라 줍시다. 방법은 위와 똑같습니다. $f(x) = y$ 로 놓고, $y$ 에 대해 같은 방법을 사용하겠습니다.

\begin{equation*} \begin{aligned} \log_2(y) &= \log_2 \left( 1 + \frac{M_y}{2^{23}} \right) + E_y - 127 \\ &\approx \frac{M_y}{2^{23}} + \mu + E_y - 127 \\ &= \frac{1}{2^{23}} \left( M_y + 2^{23} E_y \right) + \mu - 127 \\ &= \frac{1}{2^{23}} \cdot y' + \mu - 127 \end{aligned} \end{equation*}

이제 둘이 붙여서 풀어 주겠습니다!

\begin{equation*} \begin{gathered} \frac{1}{2^{23}} \cdot y' + \mu - 127 = -\frac{1}{2^{24}} \cdot x' - \frac{1}{2}(\mu - 127) \\ \frac{1}{2^{23}} \cdot y' = -\frac{1}{2^{24}} \cdot x' - \frac{3}{2}(\mu - 127) \\ y' = -\frac{1}{2} x' + 3 \cdot (127 - \mu) \cdot 2^{22} \\ y' = 3 \cdot (127 - \mu) \cdot 2^{22} - \frac{1}{2} x' \end{gathered} \end{equation*}

마지막 줄을 잘 봐주십시오. $y$ 의 정수 표현식은 상수에다가 $x$ 의 정수 표현식을 반띵해서 뺀 값입니다.

즉, 상수(0x5F3759DF)에다가 $x$ 의 정수 표현식(i)을 반띵(<< 1)해서 뺀 값… 문제의 코드와 완전히 똑같은 내용이 아닙니까!

실제로 이 코드에서 사용하는 $\mu$ 값은 $\mu = 0.04504656$ 입니다.

그런데 왜 나눗셈을 할 때 시프트 연산자를 사용하는 걸까요?

시프트 연산자는 어떤 크기의 이진수 문자열을 왼쪽 또는 오른쪽으로 몇 칸씩 옮기는 역할을 합니다. 여기서 저장공간 바깥으로 흘러넘치는 비트는 버리고, 빈 공간은 0으로 채워넣죠.

예를 들어, 1바이트 수 11010110₍₂₎을 왼쪽으로 시프트(a.k.a. shl)하면 10101100₍₂₎이 되는 것입니다!

같은 개념을 10진수에 적용해보면 나눗셈 대신 시프트를 사용하는 이유도 바로 보입니다.

159,259라는 10진수 수를 생각해 보겠습니다. 이 수를 왼쪽으로 1회 시프트하면 1,582,590이므로 원래 수에 10을 곱한 것과 같고, 반대로 오른쪽으로 1회 시프트하면 15,825로 원래 수를 10으로 나눈 것과 같습니다. (정수 나눗셈을 의미하므로 나머지는 버립니다.)

즉, 어떤 $n$ 진수 수 $a$ 에 대하여, $a$ 를 $k$ 회 왼쪽으로 시프트하는 것은 $a$ 에 $n^k$ 를 곱하는 것과 같고, $a$ 를 $k$ 회 오른쪽으로 시프트하는 것은 $a$ 를 $n^k$ 로 나누는 것과 같습니다!

특히, 이진수를 사용하는 컴퓨터의 경우 어떤 수를 1회 시프트하는 것은 CPU 사이클을 1회밖에 사용하지 않습니다. 반대로, 나눗셈(x86 ISE의 div 명령)은 CPU 사이클 1회로 끝나는 단발성 연산이 아닙니다. ECX 레지스터를 카운터로 사용해서 같은 수를 여러 번 빼는 방식으로 구현되어 있기 때문입니다.

예를 들어, 6을 2로 나누려면 먼저 6 - 2 = 4 (ecx = 1), 그 다음 4 - 2 = 2 (ecx = 2), 마지막으로 2 - 2 = 0 (ecx = 3)을 계산해서 나눗셈 결과인 3을 알아내는 것이죠.

아무리 컴퓨터의 연산이 빠르다지만, 2로 나누는 작업은 말 그대로 이진수 단위에서 지원하는 연산이니 굳이 느린 div 명령을 사용할 필요가 없는 겁니다!

이렇게 말 그대로 욕 나오는 코드 한 줄을 해석해 보았습니다. 이렇게 하면 y에는 우리가 원하는 결과가 들어가지 않았겠습니까?

……아직은 아닙니다.

step 3. newton-raphson iteration

왜냐하면 아직 우리가 원하는 만큼의 정확도를 확보하지 못했기 때문입니다.

방금 전 단계에서 이것저것 수식을 갖다 썼지만, 저 식에는 많은 오차가 있습니다.

로그함수를 근사하기 위해 일차함수를 갖다 썼고,
일차함수의 보정값 역시 원래는 0x5F3759DE.823에 가까운데 그냥 소숫점을 버렸기 때문입니다.

그래서 아직 실제 정규화 식에 적용하기에는 조금 오차가 너무 큰 것입니다.

그러면 오차는 어떻게 보정할까요? 아래 코드를 사용해서 보정합니다.

    y = y * (threehalfs - (x2 * y * y));    // 1st iteration
//  y = y * (threehalfs - (x2 * y * y));    // 2nd iteration, this can be removed

이 단계의 제목에서도 보셨겠지만, 이미 여기서 사용하는 오차 보정법은 위에서 다뤘습니다. 맨 처음 도입부의 뉴턴-랍슨 근사법을 기억하십니까? 그겁니다, 그거.

뉴턴-랍슨 근사법의 식을 한번 다시 보겠습니다.

\begin{equation*} x_{n + 1} = x_n - \frac{f(x_n)}{f'(x_n)} \end{equation*}

여기서 $x_n$ 은 $n$ 번째 어림값, 그리고 $x_{n+1}$ 은 $f(x)$ 의 근에 더 가까운 어림값입니다.

여기서 중요한 포인트는 바로 뉴턴-랍슨 근사법은 미분 가능한 임의의 함수 $f(x)$ 의 근을 찾는 알고리즘이라는 것입니다.

즉, $f(x) = 0$ 이게 하는 $x$ 를 어림하는 것이죠! 따라서 우리가 아까 작성한 제곱근의 역수를 구하는 함수 $f(x)$ 를 바로 넣을 수는 없습니다.

그러면 위 근사법을 사용할 수 있도록 식을 변형시켜 주겠습니다. $x$ 의 제곱근의 역수 $f(x)$ 를 $y$ 라고 두고, $x$ 에 대해 정리하겠습니다.

\begin{equation*} \begin{gathered} y = \frac{1}{\sqrt{x}} \\ \frac{1}{y} = \sqrt{x} \\ \frac{1}{y^2} = x \end{gathered} \end{equation*}

우변의 $x$ 를 좌변으로 넘깁니다.

\begin{equation*} \frac{1}{y^2} - x = 0 \end{equation*}

여기서 $x$ 의 값은 Q_rsqt의 매개변수로 주어져서 우리가 이미 알고 있지만, $y$ 의 값은 계산하지 않으면 알 수 없는 값입니다. 즉, 우리가 어림해야 하는 변수는 $y$ 인 것이죠. 그러니 $x$ 를 상수, $y$ 를 독립변수로 취급해서 함수 $g$ 를 만들어 보겠습니다.

\begin{equation*} g(y) = \frac{1}{y^2} - x \end{equation*}

뉴턴-랍슨 근사법은 어떻게 보면 경사하강법(gradient descent)의 일종이라고 볼 수 있습니다. 그러니 경사, 즉 기울기를 구해야겠죠? 함수 $g$ 를 $y$ 에 대해서 미분합니다.

\begin{equation*} \frac{d}{dy} g(y) = -\frac{2}{y^3} \end{equation*}

이제 뉴턴-랍슨 근사법을 사용해서 함수 $g$ 의 근을 어림합니다.

\begin{equation*} \begin{aligned} y_{n+1} &= y_n - \frac{\frac{1}{y_n^2} - x}{-\frac{2}{y_n^3}} \\ &= y_n + \frac{y_n}{2} - \frac{xy_n^3}{2} \\ &= y_n \left( \frac{3}{2} - \frac{xy_n^2}{2} \right) \end{aligned} \end{equation*}

이렇게 코드와 똑같은 식을 유도해낼 수 있다는 것을 알 수 있습니다.

"아니, 이 근사법이 더럽게 느려서 그걸 개선하기 위한 게 이 알고리즘이라며? 여기서 또 쓸 거면 최적화는 왜 하는데?"

좋은 지적입니다.

정확히 말하면 이 근사법 자체가 느린 것은 아닙니다. 구하려는 함수는 정해져 있으니 사람이 직접 해석적으로 미분한 뒤 그 값을 하드코딩하면 되고, 위에서 볼 수 있듯이 1회 어림하는 데 사용하는 연산은 기본적인 실수 사칙연산이거든요.

문제는 바로 이 근사법이 경사하강법과 비슷하다는 점에서 기인합니다.

함수값과 그 미분값을 바탕으로 국소적인 최소점(local minumum)을 향해 점진적으로 어림값을 갱신하는 이 알고리즘의 특성상, 같은 연산을 적게는 몇 번에서 많게는 수십 번까지 반복해야 한다는 점이 바로 문제인 것입니다. 당시 CPU의 둥둥 소수점 실수 연산 속도가 정수 연산 속도보다 현저히 느렸다는 점도 한몫하여, 이 계산을 실시간으로 몇 천 번씩 수행하는 건 조금 부담이 있었죠.

다만 이 경우 비트 단위 흑마법을 통해 충분히 가까운 어림값을 구해 냈고, 약간의 미세조정만 거치면 되므로 이 근사법을 사용한 것입니다. 조금 더 정확한 결과를 위해서는 주석으로 표시된 부분을 살려서 2회 어림을 했겠지만 (2nd iteration이 그래서 적혀 있습니다), 32비트 둥둥 소수점 범위 내에서는 사실상 무시 가능한 수준으로 최적화가 이루어지니 굳이 CPU 사이클을 낭비할 필요가 없는 거죠.

마치며

이 알고리즘은 한동안 게임엔진에서는 빠질 수 없는 코드로 통용되었습니다. 제곱근을 계산하는 데 너무나도 효율적인 방법이었기 때문입니다. 하지만 요즘은 이 코드가 자주 쓰이지는 않습니다. 그 이유는 당연히…

요즘 CPU에 이미 탑재되어 있는 기능이기 때문입니다.

x86과 amd64 ISA의 경우, SSE 확장이 적용되면서 제곱근을 구하는 FPU 명령어가 기본으로 제공되고, ARM같은 RISC 시스템에서도 제곱근 명령어가 제공됩니다. 심지어 RISC-V같은 시스템에서도 fsqrt.s 명령어가 제공되는 시점에, 굳이 코드로 이걸 구해낼 필요가 없어졌죠.

거기다 벡터 연산 역시 SIMD(single-instruction multiple-data) 명령어를 사용해서 CPU 사이클 몇 개 안에 구해내는 시점에 이런 하드코딩 알고리즘이 들어설 자리는 많이 사라졌습니다.

요즘은 수학을 이용한 알고리즘에 대한 흥미를 불러일으킬 때 자주 사용되는 것 같습니다.

약간… 문제지의 챕터 사이에 있는 쿠키 페이지 느낌으로?

신기하게 생겼다 보니 흥미 유발에는 제격이라나 뭐라나 그렇답니다.

아무튼, 지금까지 전설적인 프로그래머의 전설적인 알고리즘에 대해 알아보았습니다.

재밌게 보셨는지 모르겠습니다. 내용이 너무 씹ㄷ…매니악해서 대상 독자의 범위가 좁은지라…

프로그래밍에 입문할 만한 글은 아니지만, 이걸 보시고 프로그래밍에 흥미를 가져 보셨으면 좋겠습니다.

프로그래밍 입문용 게시글은 여기저기 많이 보이는 것 같으니……

저야 컴퓨터에 흥미가 많아서 프로그래밍을 시작했지만, 역시 무언가를 배운다는 건 즐거운 일 아니겠습니까?

그러면 저는 조만간 새로운 흑마법으로 찾아뵙겠습니다.

필승!

다음편 예고

"루프를 스위치에 싸서 드셔보세요."

"¿?"

TO BE CONTINUED…